【第5回】定量的な裏づけ-標本数:サンプルサイズ(標本数)の考え方について
調査の信頼性を高めるために
サンプルサイズの考え方とロジカルシンキング
「みんなって誰?」「それでホントにみんなって言えるの?」をきちんと、ロジカルに説明していこうとすれば、定量的に信頼性の高いデータの確保が不可欠になります。
では、「定量的に信頼性の高いデータ」とは、具体的に、どれだけの”数”のデータを集めれば良いのでしょうか?
サンプルサイズ(標本数)の設定は、まさにこの問題です。
これは、ロジカルに考える問題であるとともに、「判断の問題」でもあります。
統計的な信頼度はもちろん、数に比例して高くなります。
ただし、無制限にサンプルサイズを増やせば、当然ながらその分の費用は上がります。
調査を実務面から考え、予算と信頼性の兼ね合いを見ながら、結果として役立つ数(標本数)を設定することが肝要です。
サンプルサイズの決定も、ロジカルに行きましょう。
必要サンプルサイズの算出方法は、一般的には、次のようなステップです。
サンプルサイズの算出ステップ
▼STEP1.許容誤差範囲の決定
どの程度までサンプリング誤差を許すのか、誤差の範囲を決める
許容誤差範囲とは?:
もし、対象者全員に調査を行った場合に得られるであろう測定結果(真値)との許せる誤差の範囲のこと。
±10%程度でもおおよその結果がわかればよしとするのか、±3%程度の精度の高いデータが欲しいのか、を判断するということ
▼STEP2.予算との兼ね合いによるサンプルサイズの算定
サンプルサイズが多いほど精度は高くなるが、費用もその分高くなるため、予算も考えながら、調査結果が、一定の誤差範囲に収まるようにするためのサンプルサイズを算出する
系統抽出法など、無作為抽出法の誤差を数式で表すと、以下となります。
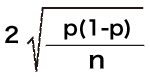
n=サンプル数
p=ある質問に対する回答比率
「2」は信頼度95%の係数1.96の近似値
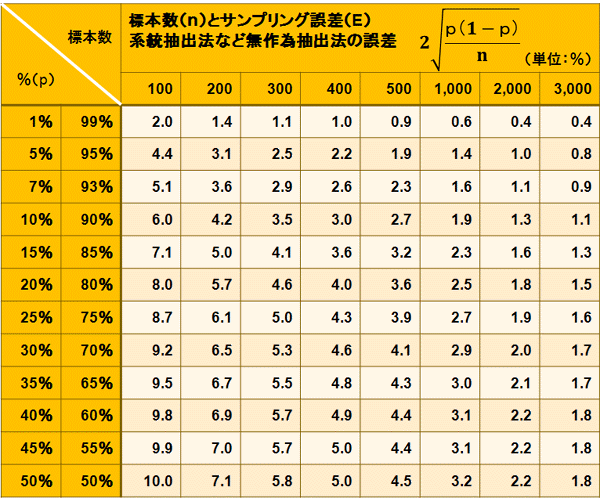
回答比率の誤差と、サンプルサイズとの関係を示したものが下記の表です。
この表は、無作為抽出で「サンプルを○○件とり(下表横軸)、その結果○○%の回答が得られた場合(下表縦軸)にプラス・マイナス何%の誤差があるか」をあらわしたものです。
必要な調査対象サンプルサイズ(標本数)の求め方(サンプリング誤差早見表)
●パーセントのサンプリング誤差の早見表(5%水準の危険度=信頼率95%)
- 調査設計におけるサンプル数(標本数/n)の導き出し方
この表では信頼率95%をベースとしており、20回調査をすると、19回は同じ結果が得られることを意味します。
信頼率とは:
全数調査と比較して、どの程度、信頼できるデータなのかを示す規準。
一般的にはおおよそ、95%以上の確率で許容誤差範囲内に測定値が収まれば良しとする、と考えます。
この「○○%以上」という基準値を信頼率と言います。
統計的に見て、最も誤差が生じやすいのは、回答比率が「50%」のときです。
例えばある商品に対して満足している割合が50%の場合、n=100にした場合では、50%±10%、つまり、正しい値は40%~60%の間にあると見なします。
もし、これを同じ条件で、 回答誤差を±10%から、その半分の±5%にするためには、n=100から、n=400、つまりサンプル数を4倍にしなければなりません。
一方で、n=1000を、2倍のn=2000にしたとしても、その誤差は、±1%程度しか変りません。
この、誤差をどの範囲まで認めるか、調査結果にどれだけのデータ信頼度を求めるかが、サンプルサイズを考える上での基準になります。
クロス集計を考えたサンプルサイズの設定について
サンプルサイズの設定については、あわせてクロス集計(質問項目間の集計)について、分析軸の考え方を事前に整理しておくことが不可欠です。
大まかに全体傾向がわかれば良いのか、47都道府県別にまで落とし込んだ分析にも耐えうる情報が欲しいのか、など、調査結果の役立て方によって、サンプルサイズの設定は大きく異なります。
例えば、全体分析をおおまかに掴みたいということが調査目的ならば、全国で500サンプルもあれば十分な調査かもしれませんが、500サンプルを後から47都道府県で分析しようとしても、1都道府県あたり、単純に500÷47で、n=10程度。
わずか、10件程度のデータで、「北海道はxxx、東京は、yyy・・」と語っても信頼性はありません。
最終的に調査結果をもとに、都道府県別にアクションプランを考えることを目的とするならば、信頼性の面から、少なくとも、n=100×47 おおよそ、n=5,000と、当初考えていたn=500の10倍の数が必要です。
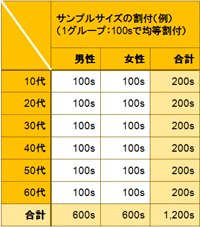
KFSでは、クロス集計を考えると、1グループ100サンプルが望ましい値、最低でも、1グループ50サンプルは必要
と考えています。
例えば、単純に、性別・年齢別にクロス集計で大まかな傾向を知り、属性間の違いを知りたい、などといった場合、均等割り付けで考えると左記のような割付になります。
望ましいサンプルサイズ:1グループ(n=100)×性・年齢カテゴリー数12=(n=1,200)
最低限だが分析可能:1グループ(n=50)×性・年齢カテゴリー数12=(n=600)
上記の割付では、各性別×年齢の1グループごとに(n=100)ずつの均等割付ですが、母集団の属性に基づく標本割付を行うこと(前回指摘の「代表性の問題)」についても、注意が必要です。
商品特性によって、ユーザーの属性は異なります。
例えば、購入者の半数以上が50代である商品で実態調査を行いたいのであれば、50代以上を回答者の50%の標本数とする、それよりも、今後のターゲットとなりうる30~40代について、重点的に知りたいのならば、30~40代に比重をかけたサンプル数にする、といった目的に沿った対象の選び方が必要となります。
調査設計の重要性について、何度も語っているのは、
どのように調査を役立てたいのか、上位目的と下位目的の関係は? といった点が明確化されていないと、この分析軸やサンプルサイズの設定方法が詰めきれず、なんとなく予算優先で決まってしまう、結果、せっかく調査をしたのに、調査をした後、「この結果は信頼できない、参考値で」といった中途半端な分析しかできないことが起こりうるからです。
また、あわせて母比率(出現率)は、調査予算に影響を与えるので、留意しておいたほうが良いでしょう。
- 母比率とは:
ある性質を持つものが母集団においてどれくらいかを占める比率。
例えば、自動車の所有率と、自家製クルーザーの所有率は違うように、母比率が異なれば、調査対象者を発見する難易度が異なるため、調査費用に影響します。
ただ注意をして欲しいのは、「みんなって誰?」「それでホントにみんなって言えるの?」をロジカルに追っていくと、「正確な信頼性の置ける調査をやること」にどうしても視点が行過ぎてしまうこと。
定量的な裏づけのないデータは、説得材料にも、判断材料にもなりませんが、「調査としての完璧さを追い求めること」、これが目的化してしまっては本末転倒になってしまいます。
調査をやること自体が目的ではなく、調査を生かして意思決定をしていくことが目的だったはずなのですから。
結サンプルサイズをどうするかは、自身のデータの分析・活用イメージ(目的)に対して、そのデータの信頼性・精度をどのレベルで良しとするか、といった最終的には判断・割り切りの問題です。
本格調査の前のプレ調査といった位置づけ、多くの資料のうちの判断材料の1つとして、ポイント的に裏づけの取れるデータが入手できれば良しとする場合と、「この情報をベースに、今後の中長期計画を立てる」では、求められる情報の精度が異なるのは当然であり、割り切るベき時は割り切ることが必要です。
「目的思考」こそ、ロジカルシンキングの原点です。
*実際には限られたサンプルであるのに、世の中全体を現しているように一般化して、事実誤認を引き起こす現象を、「過剰一般化のバイアス」と呼びます。
詳しく知りたい方はこちら→過剰一般化のバイアス (少数の法則)
まとめ:サンプルサイズ(標本数)の考え方
調査の際に、必要なサンプルサイズを考えることは、ロジカルに考える問題であるとともに、「判断の問題」です。
一定の信頼性を得るために必要なサンプルサイズの数自体は、ある意味、自動的に、数式で求められます。
ただ、そのサンプルサイズを最終的に決めるためには、調査母集団に対する理解と、自身のデータの分析・活用イメージ(目的)に対して、
- どこまで調査母集団の代表性に迫ったデータが欲しいのか
- そのデータの信頼性・精度をどのレベルで「良し」とするか
費用も踏まえ、判断(割り切り)が必要となってくるのです。
調査を実施する前の調査設計の段階で、この点をきちんと議論しておくことが、役に立つ調査をする上での要件です。
リサーチとロジカル&ラテラルシンキング・コンテンツ
はじめに:リサーチと思考法
【第1回】So What?/Why So?(調査目的の明確化)
【第2回】調査設計とロジカルシンキング
【第3回】Fact&Stick:定量調査と定性を組み合わせた ハイブリット調査の薦め(調査手法)
【第4回】みんなって誰?-代表性(調査対象者の選定)
【第5回】定量的な裏づけ-標本数:サンプルサイズ(標本数)の考え方について
